瓜瓜小屋
0%

发表于 更新于 分类于 ，

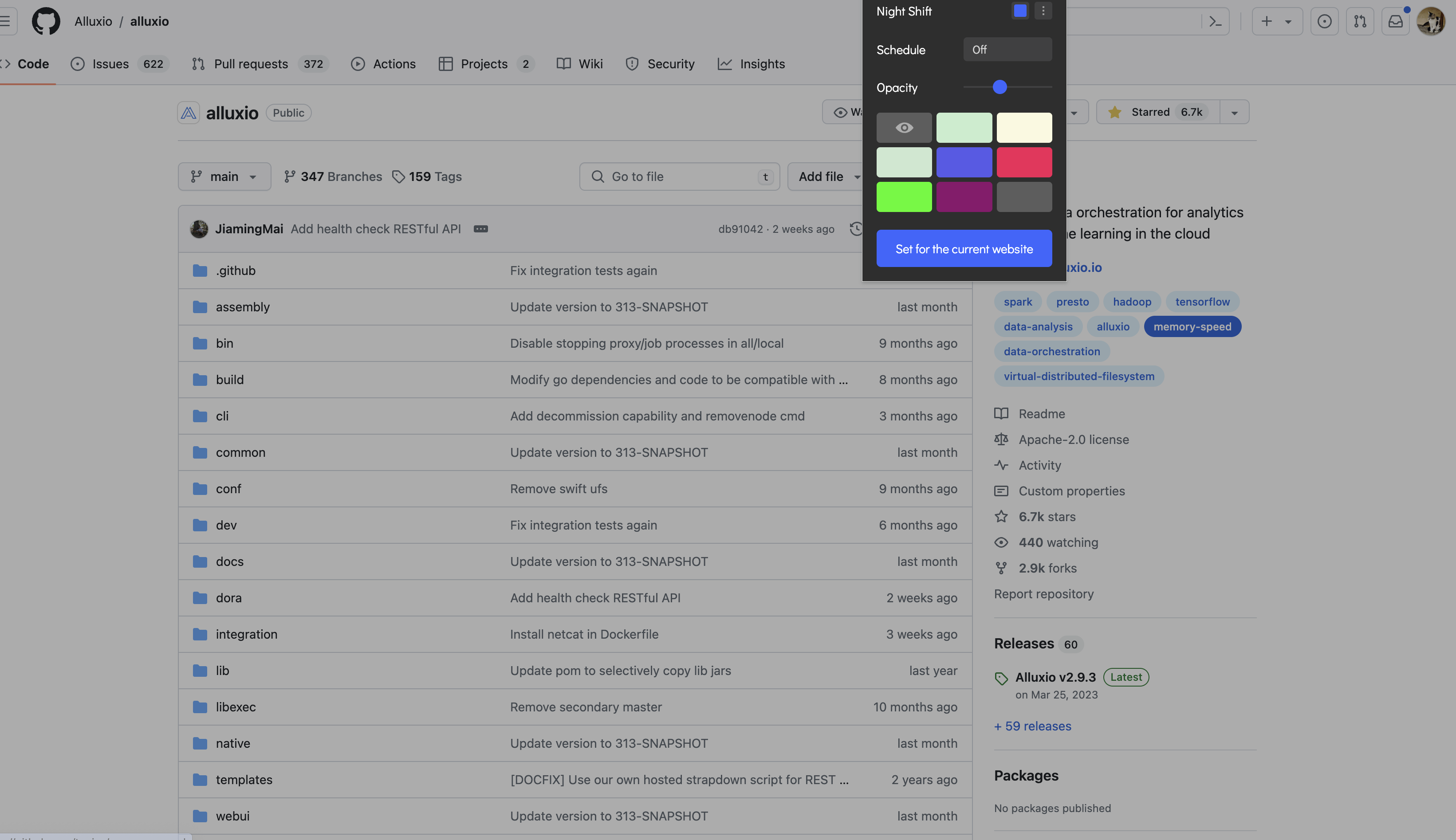
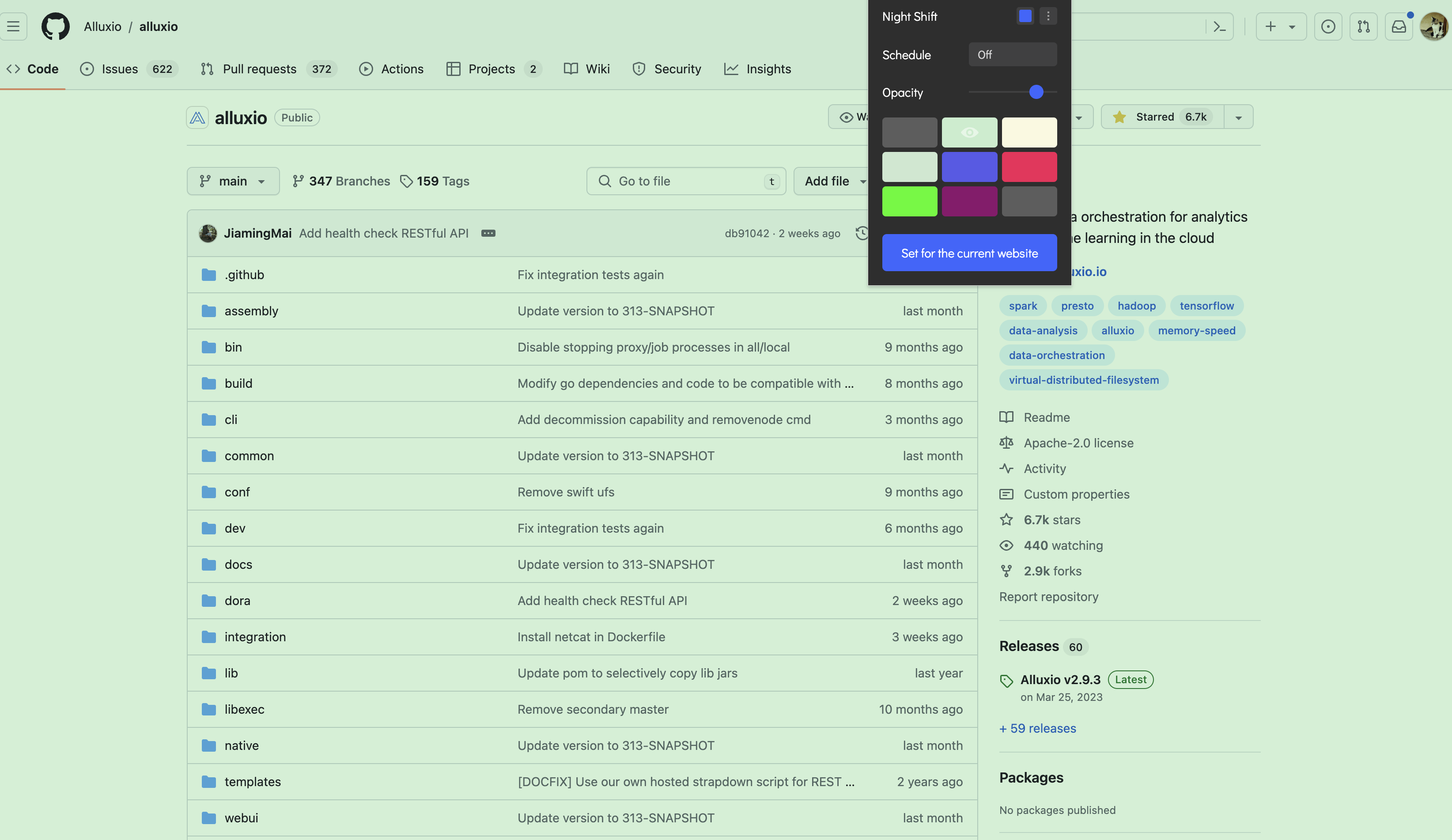
Alluxio在帮助统一跨各种平台用户数据的同时还有助于为用户提升总体 I/O 吞吐量。

Alluxio是通过把存储分为两个不同的类别来实现这一目标的。

  • UFS(底层文件存储，也称为底层存储)
    • 该存储空间代表不受Alluxio管理的空间。 UFS存储可能来自外部文件系统，包括如HDFS或S3。
    • Alluxio可能连接到一个或多个UFS并在一个命名空间中统一呈现这类底层存储。
    • 通常，UFS存储旨在相当长一段时间持久存储大量数据。
  • Alluxio存储
    • Alluxio做为一个分布式缓存来管理Alluxio workers本地存储，包括内存。这个在用户应用程序与各种底层存储之间的快速数据层带来的是显著提高的I/O性能。
    • Alluxio存储主要用于存储热数据，暂态数据，而不是长期持久数据存储。
    • 每个Alluxio节点要管理的存储量和类型由用户配置决定。
    • 即使数据当前不在Alluxio存储中，通过Alluxio连接的UFS中的文件仍然对Alluxio客户可见。当客户端尝试读取仅可从UFS获得的文件时数据将被复制到Alluxio存储中。

Alluxio存储通过将数据存储在计算节点内存中来提高性能。Alluxio存储中的数据可以被复制来形成”热”数据，更易于I/O并行操作和使用。

Alluxio中的数据副本独立于UFS中可能已存在的副本。 Alluxio存储中的数据副本数是由集群活动动态决定的。 由于Alluxio依赖底层文件存储来存储大部分数据， Alluxio不需要保存未使用的数据副本。

Alluxio还支持让系统存储软件可感知的分层存储，使类似L1/L2 CPU缓存一样的数据存储优化成为可能。

🟠所以，Alluxio本质上是一个中间层。

阅读全文 »

发表于 更新于 分类于 ，

MLPerf

吞吐量、IOPS 和延迟 Q&A

引用自：https://mp.weixin.qq.com/s/Yz2lkYzimfFC-85KBUq_zQ

吞吐量、IOPS 和延迟是三个术语，通常称为存储性能指标。

SNIA 网络存储论坛 （NSF） 通过现场网络研讨会“您想知道的有关存储但太自豪而无法询问的一切”

带回了我们广受欢迎的网络研讨会系列“您想知道的有关吞吐量、IOPS 和延迟但又太自豪而无法询问的一切”。

阅读全文 »

发表于 更新于 分类于 
1
2
3
4
## 生成ssh key

```shell
ssh-keygen -t rsa -C “account-1@gmail.com”

假设账号account1生成的密钥保存在~/.ssh/id_rsa和~/.ssh/id_rsa.pub

1
ssh-keygen -t rsa -C “account-2@gmail.com”

假设账号account2生成的密钥保存在~/.ssh/id_rsa_another和~/.ssh/id_rsa_another.pub

阅读全文 »

发表于 更新于 分类于 ，

本篇讲一些其他博客没有展开讲的部分。

Q：什么是lowbit函数?

A：lowbit可以取出一个数字的最低位1，如lowbit(10102{1010}_2) = 00102{0010}_2

lowbit(5) = 1,lowbit(6) = 2

Q：为什么树状数组的划分使用lowbit？

树状数组和线段树一样，需要将一个区域[1,n]分成多段

线段树的划分是：二分，需要4倍内存(粗略4倍)

而树状数组的划分是：二进制分解

假设n=2i1+2i2+…+2imn = 2^{i_1}+2^{i_2}+…+2^{i_m}

那么对于[1,n][1,n]的区域，划分的区间为：

[1,2i1][1,2^{i_1}]

[2i1+1,2i1+2i2][2^{i_1}+1,2^{i_1}+2^{i_2}]

……

[2i1+2i2+…+2im−1+1,2i1+2i2+…+2im],[2^{i_1}+2^{i_2}+…+2^{i_{m-1}}+1,2^{i_1}+2^{i_2}+…+2^{i_{m}}],

x=7=20+21+22x = 7 = 2^0+2^1+2^2

1
2
3
4
5
6
7
8
9
10
x = 7;
lowbit(x); // lowbit(x) = 1
x-=lowbit(x); // x = 6
lowbit(x); // lowbit(x) = 2
x-=lowbit(x); // x = 4
lowbit(x); //lowbit(x) = 4
x-=lowbit(x); // x = 0
[1,7]被划分为[1,4],[5,6],[7,7]

树状数组c[x]保存的则是：[x-lowbit(x)+1,x]区间中所有数的和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int ask(int x) {
    int ans = 0;
    while(x) {
        ans+=c[x];
        x-=lowbit(x);
        // x = 7->[7,7] , c[7] = a[7]
        // x = 6->[5,6] , c[6] = a[5]+a[6]
        // x = 4->[1,4] , c[4] = a[1]+a[2]+a[3]+a[4]
        // x = 0->end
        //由此看出，可以保证不重合的划分
        // ans=c[7]+c[6]+c[4]
    }
    return ans;
}

同时，由以上的介绍可以推出，对于c[x]节点，它的父亲结点应该是c[x+lowbit(x)]

那么更新时则为

1
2
3
4
5
6
7
8
void add(int x,int k) {
    while(x<=n) {
        c[x]+=k;
        x+=lowbit(x); 
        // Q: 为什么是x = x+lowbit(x)？
        // A: 因为它需要更新它的父节点，使得包含它的区间得以被更新
    }
}

以上的add(int x,int k)和ask(int x)实现的功能是：单点更新、区间查询

那么如果要实现单点查询和区间更新呢？考虑利用差分的思想，请看代码：

PS:单点查询为query(x)，而不是query(x)-query(x-1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 100;

int n;
int a[maxn];
int c[maxn];


int lowbit(int x) {
    return x & (-x);
}

void add(int i,int k) { // 单点更新
    while(i<=n) {
        c[i] += k;
        i += lowbit(i);
    }
}
int query(int x) { // [1,x] 区间查询
    int ans = 0;
    while(x) {
        ans += c[x];
        x -= lowbit(x);
    }
    return ans;
} 


int main() {
    int m;
    cin >> n >> m;
    for (int i = 1;i<=n;i++) {
        cin >> a[i];
    }
    for (int i = 1;i<=m;i++) {
        char c;
        cin >> c;
        if(c == 'C') {
            int l, r, d;
            cin >> l >> r >> d;
            // 区间更新
            add(l, d);
            add(r + 1, -d);
        } else {
            int x;cin>>x;
            // 单点查询
            cout << a[x] + query(x)<<endl;
        }

    }
}
阅读全文 »

发表于 更新于 分类于 ，

background

  • traditional software-based TCP/IP stack
    • 数据通过用户空间发送到远程device的用户空间。
    • 这个过程会经过若干次内存拷贝：应用缓存->kernel中的TCP协议栈缓存->驱动层->网卡缓存。
    • 多次内存拷贝需要CPU介入，处理时延大，>10us。
    • 解决方案：RDMA、TOE等。
  • hardware-based RDMA
    • from HPC to Ethernet-based datacenters
阅读全文 »

发表于 更新于 分类于 ，

快速幂方法1：
311=31×32×383^{11} = 3^1 \times 3^2 \times 3^8

1
2
3
4
5
6
7
8
9
10
long long qpow(long long x,int n,long long mod) {
    long long res = 1;
    while(n>0) {
        if(n&1) // 二进制最低位为1，则乘上x^(2^i)
            res = res * x % mod;
        x = x * x % mod;
        n >>= 1;
    }
    return res;
}
阅读全文 »

发表于 更新于 分类于 ，

扩展GCD

给定a,b

求ax=1(mod b)ax=1(mod \ b) 的最小整数解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll x, y;
ll exgcd(ll a, ll b, ll &x, ll &y){
    if(!b){
        x = 1, y = 0;
        return a;
    }
    ll d = exgcd(b, a % b, x, y);
    ll t = x;
    x = y, y = t - y * (a / b);
    return d;
}

int main() {
    ll a,b;
    cin >> a >> b;
    exgcd(a, b, x, y);
    ll ans = (x + b) % b;//最小整数解
    
    cout << ans << endl;
}
1
2
3
4
5
6
7
8
bool liEu(ll a, ll b, ll c, ll &x, ll &y) {
  ll d = exgcd(a, b, x, y);
  if (c % d != 0) return 0;
  ll k = c / d;
  x *= k;
  y *= k;
  return 1;
}
阅读全文 »

发表于 更新于 分类于 ，

1+3+5+...+(2∗n−1)=n21+3+5+...+(2*n-1) = n^2

2+4+6+...+(2∗n)=n∗(n+1)2+4+6+...+(2*n) = n*(n+1)

1+2+3+...+n=n∗(n+1)21+2+3+...+n = \frac{n*(n+1)}{2}

Cnm=Cn−1m−1+Cn−1mC_{n}^{m}= C_{n-1}^{m-1} + C_{n-1}^m

阅读全文 »

发表于 更新于 分类于 ，

Bundling

https://codingcompetitions.withgoogle.com/kickstart/round/000000000019ffc7/00000000001d3ff3

题意

将给定的n个字符串划分为大小为k的组,每组的权值为这些字符串的最长公共前缀

∑n≤106,k∣n\sum n \leq 10^6,k|n

思路

构建一棵字典树,每一个节点对应一个前缀,对于每个前缀,如果它出现的次数大于k,那么它对答案有贡献,加上即可

代码: https://xlorpaste.cn/0ve9u4

阅读全文 »